コレクション 円筒 形 体積 814534
円柱の容積は 1分でわかる意味 求め方と式 表面積の計算 体積と直径の関係
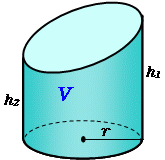
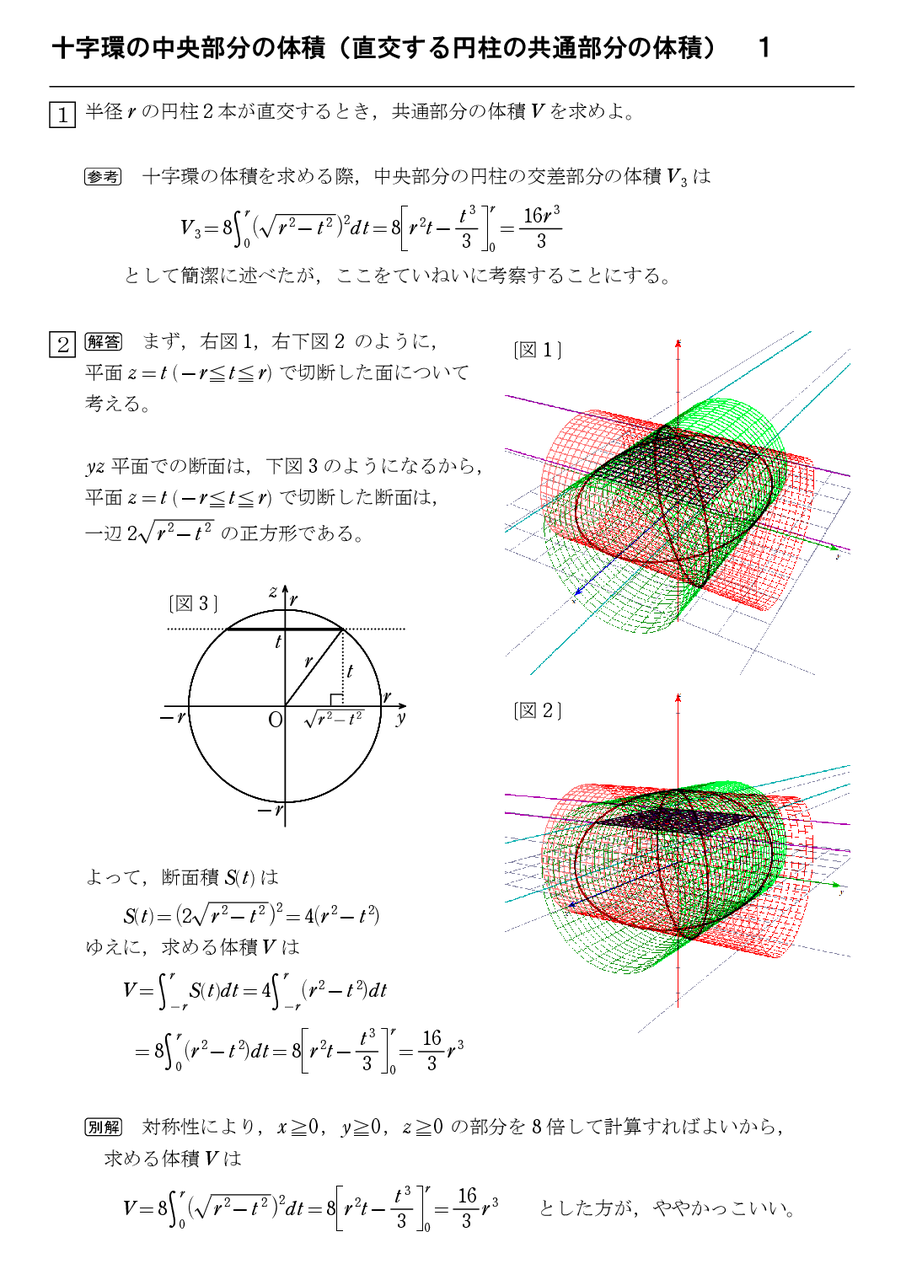
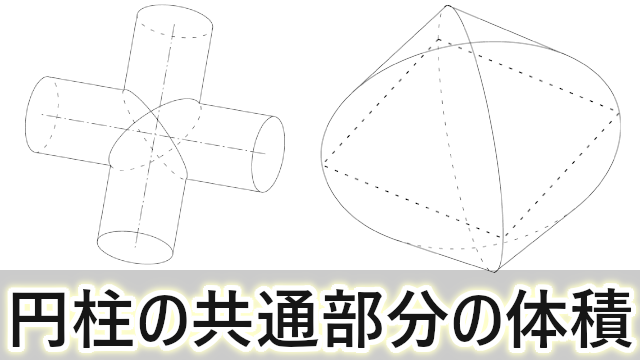
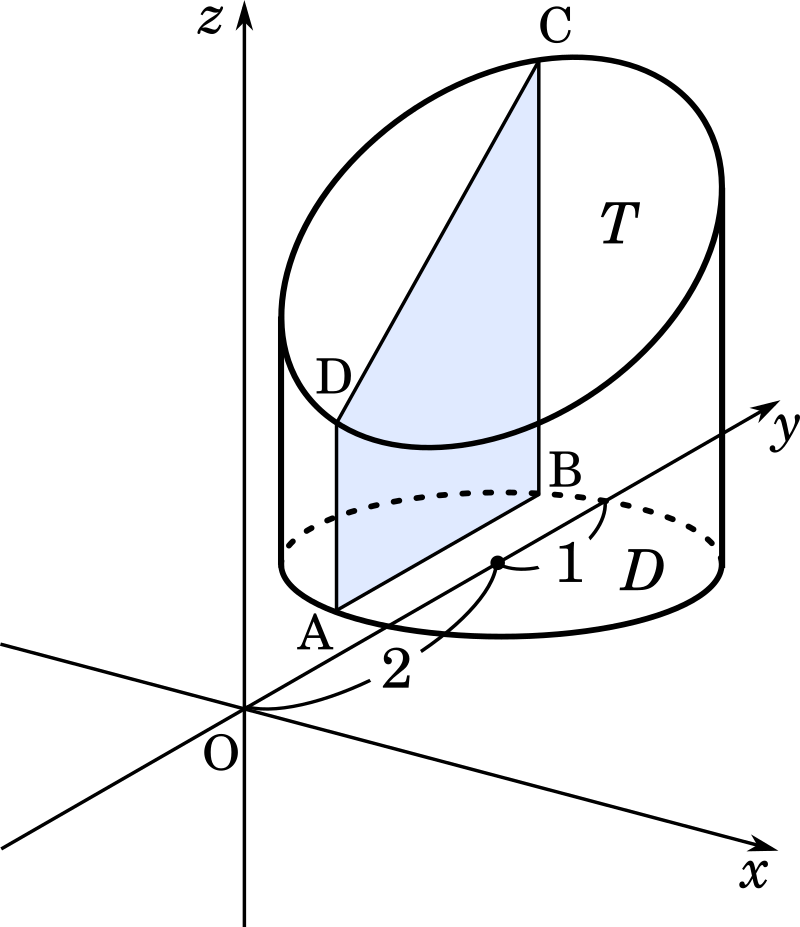
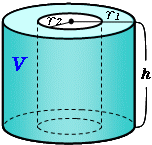
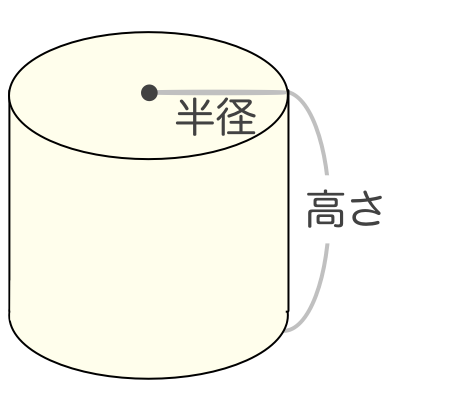
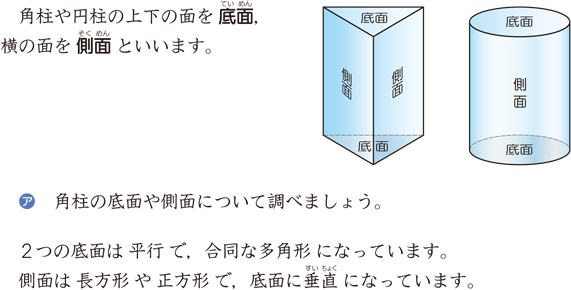
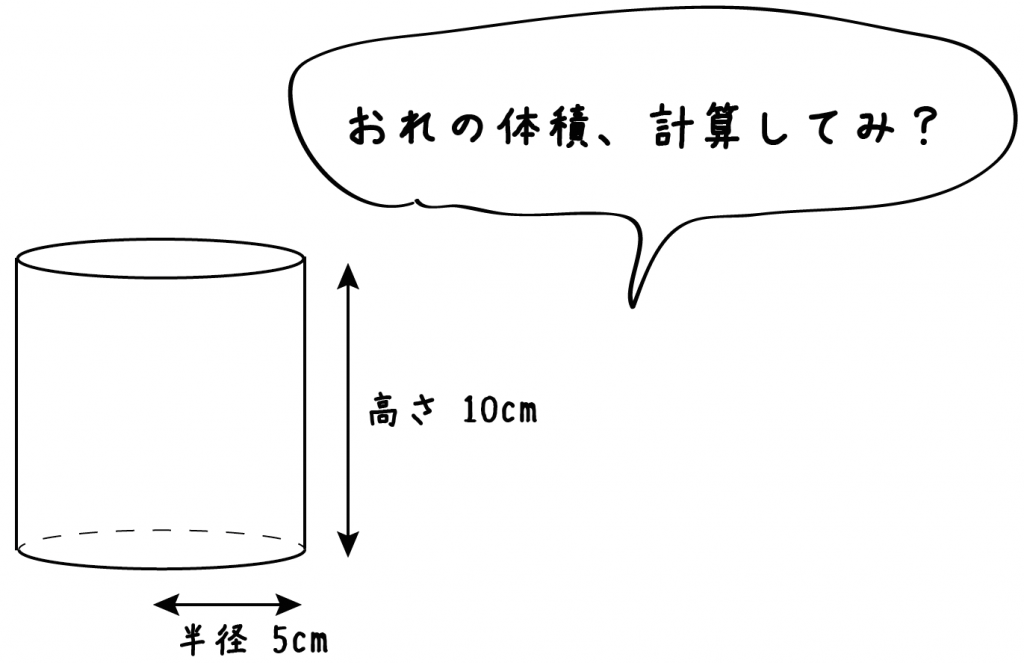
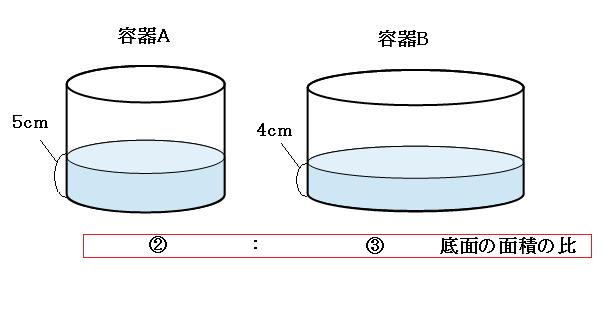
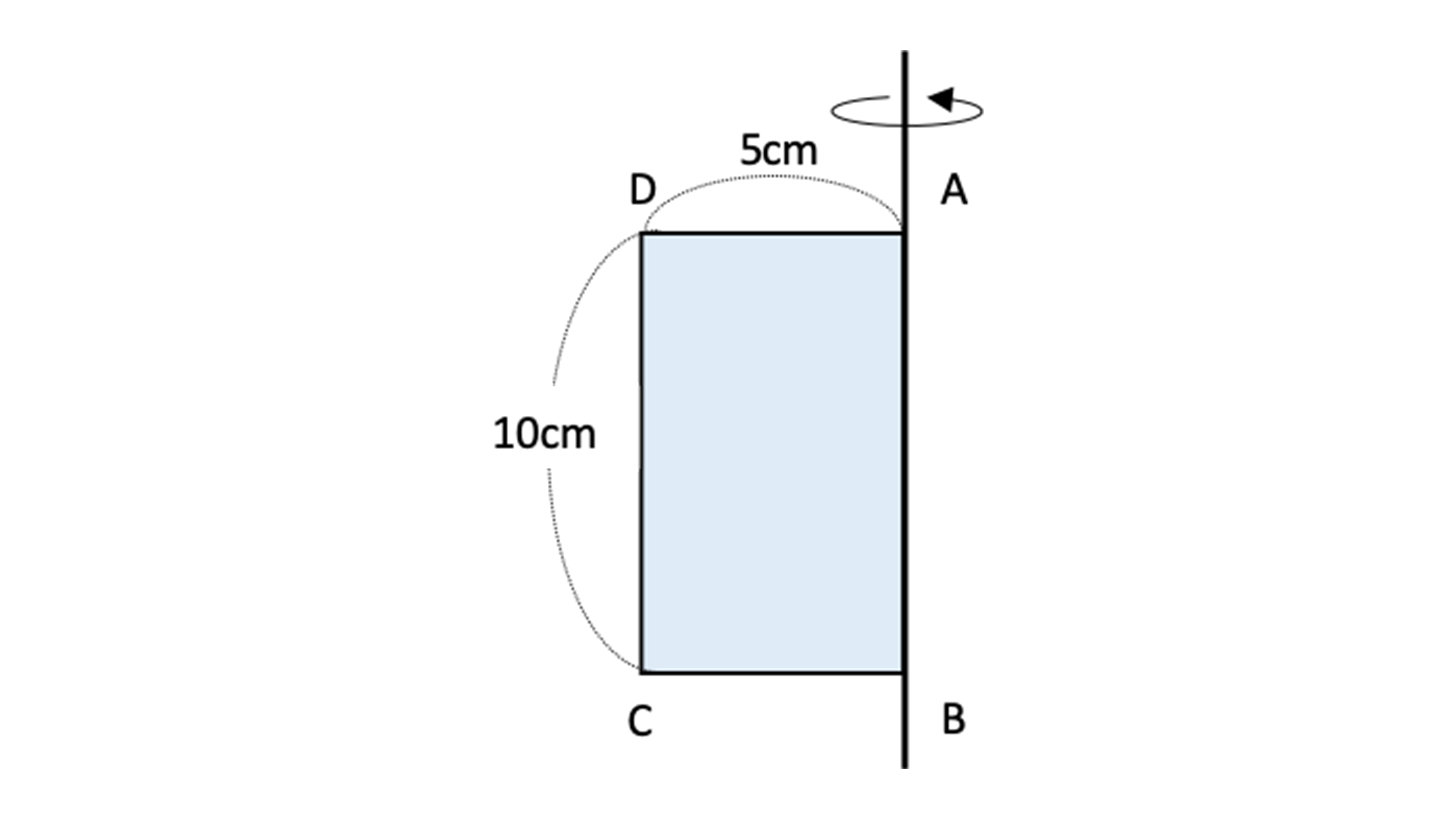
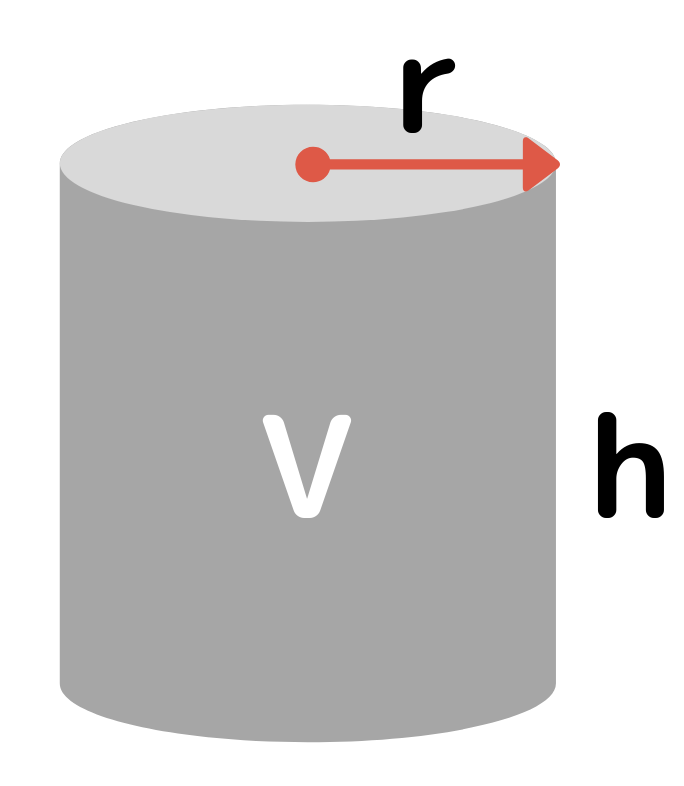
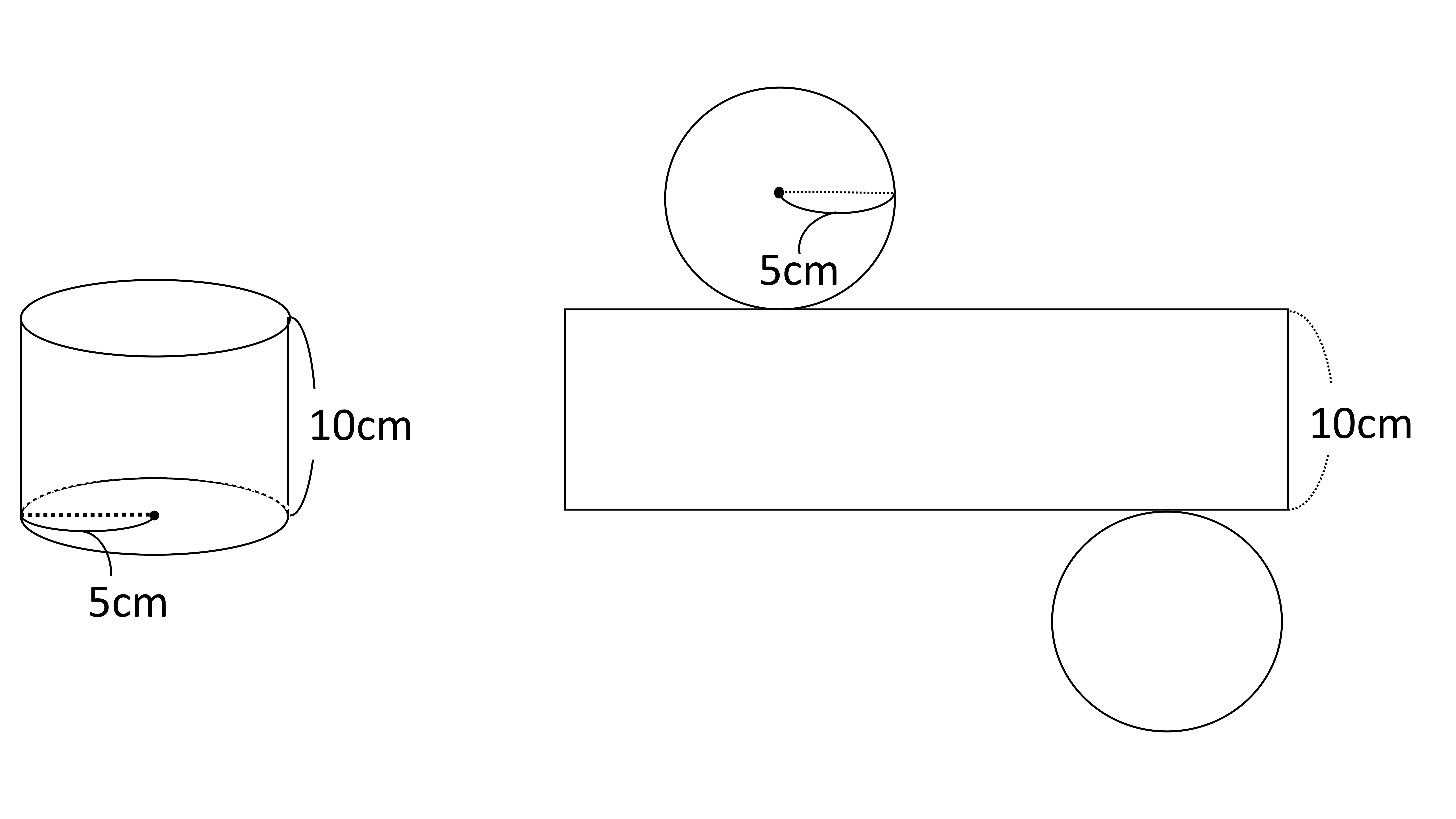
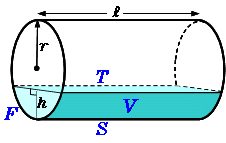
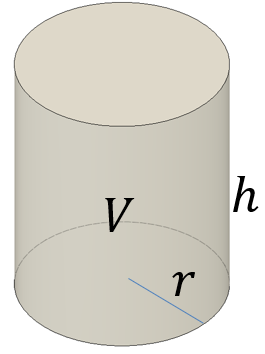
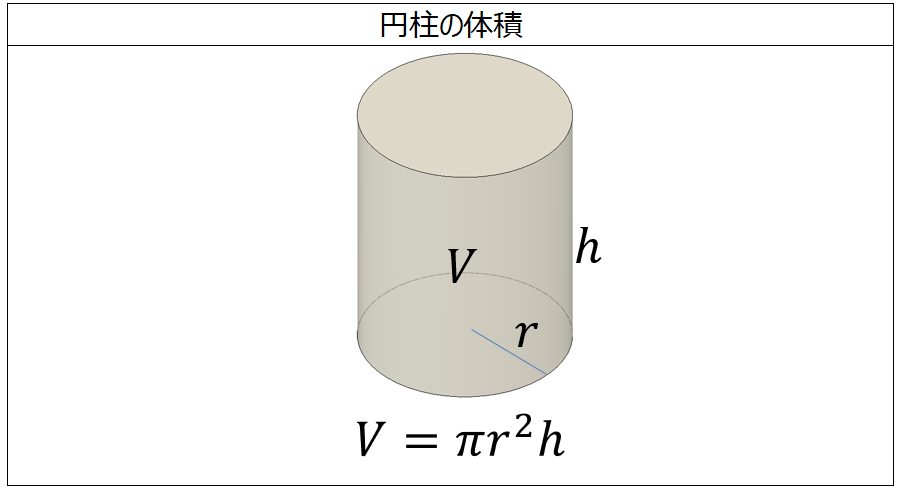
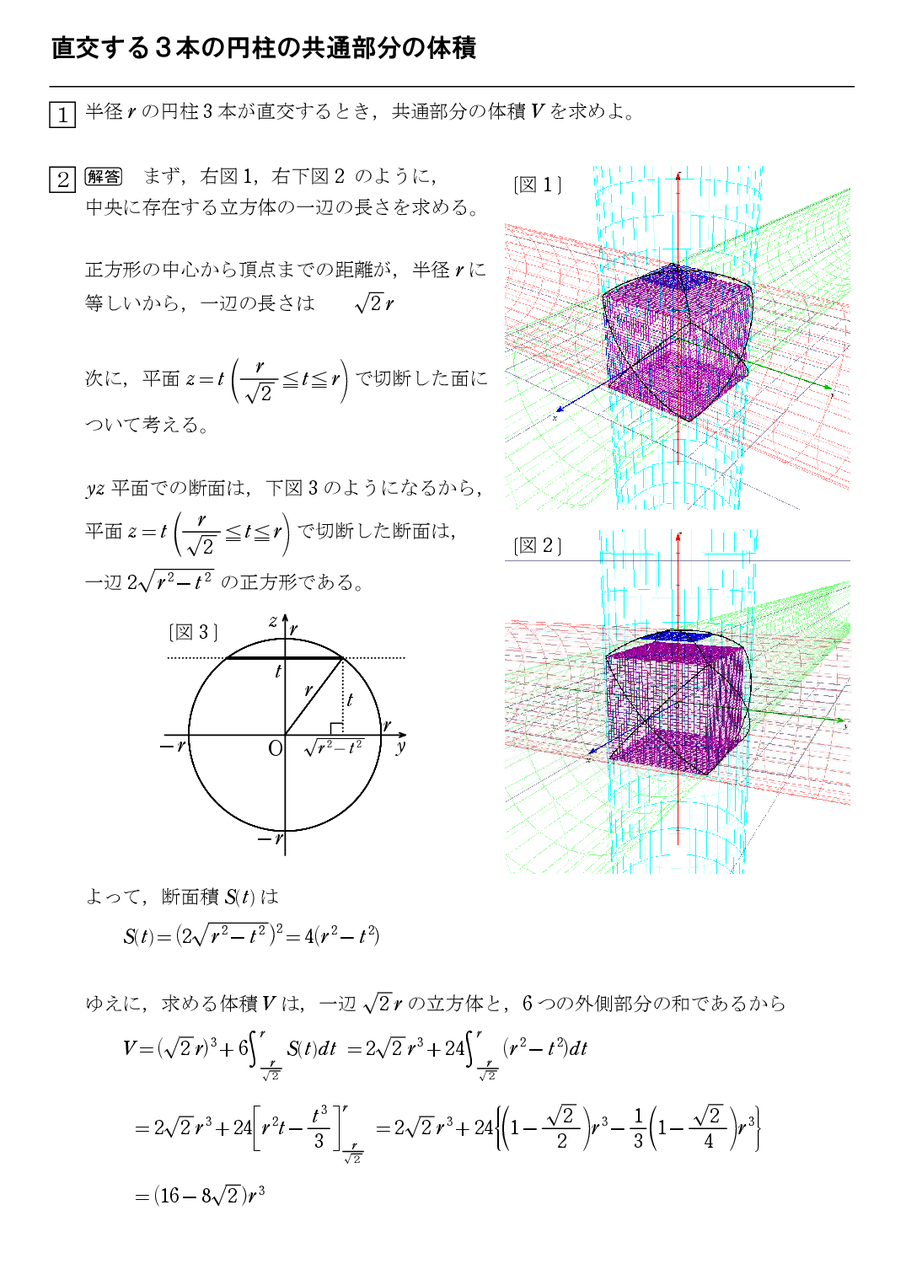
円柱の底面積 $S$ は、$S=\pi r^2$ で求められます。よって、底面の半径 $r$、高さ $h$ の円柱の体積 $V$ は、次の式で求められます。 円柱 (えんちゅう) の体積 \begin{align*} V = \pi r^2 h \end{align*} 体積 = 半径 × 半径 × 314 × 高さ直交する円筒の共通部分の体積を求める問題は,非回転体の求積問 題として,授業でもよく扱われる。しかし,共通部分の立体が,どの ような形になるかイメージできない生徒が多く,解説を聞いてもモヤ モヤ感が残り,すっきりしていないようである。そこで,ここでは, その共通部分の
円筒 形 体積
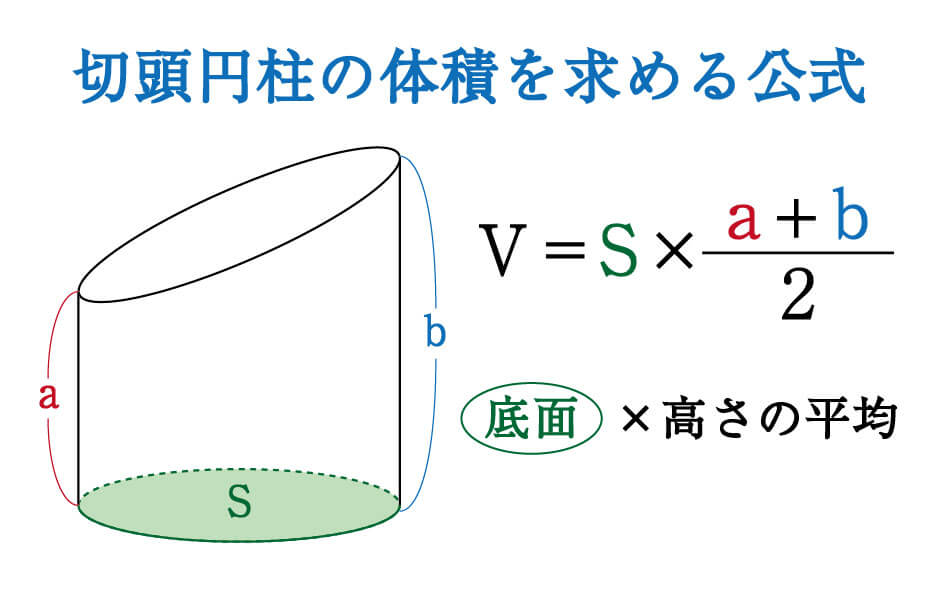
円筒 形 体積-柱体の体積\(\,V\,\)は \(\color{red}{V=(底面積)\times (高さ)}\) で求まるので体積が求められないという人は少ないです。 この計算公式は、底面の形に関係なく(円柱も三角柱も四角柱も全部)成り立ちま体積の換算 ツイート 指定された体積を他の単位の体積に変換します。 変換したい体積と単位を入力し、「体積を変換」ボタンを

円柱の表面積と体積を求める公式 具体例で学ぶ数学
二等辺三角形の2つの定理・性質 中3数学 中学数学式の展開の問題の解き方がわかる3ステップ 中1数学 ヒストグラムを使った平均値の求め方がわかる4ステップ 中1数学 簡単公式三角錐の体積の 物理学 薄肉円筒の内圧による体積変化 長さL,内径D,肉厚Hの この三角形の頂角(Cでの角度)を2θとします。 円の半径をrとして、円の中心から水面までの最短距離をhとします。つまり水面を底辺とする、二等辺三角形の高さがhです。すると h = r cos θ 三角形ABCの面積Sは S = hr sin θ よって、 S = (cosθ)(sinθ)r^2 です。一方 三角柱の体積の求め方には公式があるんだ。 三角形の底辺の長さをa、底辺からの高さをb、立体の高さがhっていう三角柱を想像してみて。 このとき、 三角柱の体積は、 1/2 abh で求めることができるんだ。 つまり、
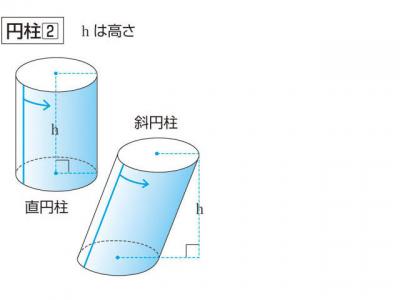
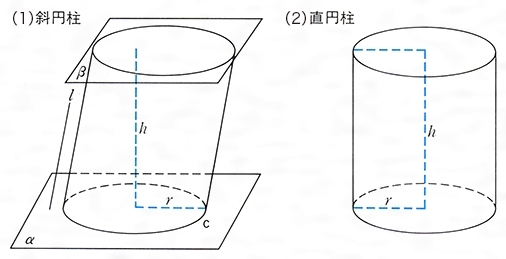
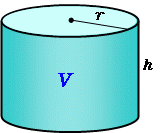
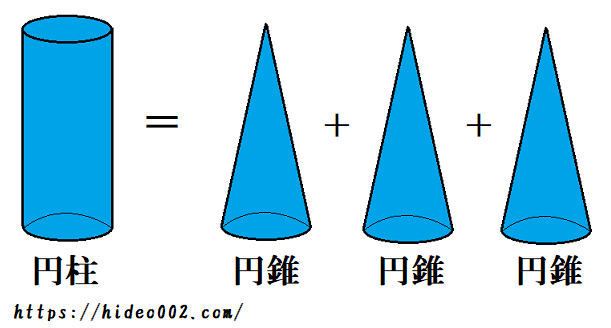
底面の半径r、高さhの円柱の体積 直円柱と斜円柱とがある。また、その形をしたもの。円柱体。円筒。 円壔(えんとう)。 ※和蘭字彙(1855‐58)「rol 円柱 温飩棒巻軸類」 出典 精選版 日本国語大辞典精選版 日本国語大辞典について 情報 デジタル大辞泉 「円柱」の解説 えん‐ちゅう〔ヱン スーちゃん 円すいの体積は円柱の3分の1ってならったよ森羅万象博士 三角すいや四角すいも3分の1になるね。なんでだろう。スーちゃん えっ正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積 直円柱の体積 一部が欠けた直円柱の体積 中空円柱の体積 斜切円柱の体積
円筒 形 体積のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
「円筒 形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「円筒 形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「円筒 形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | 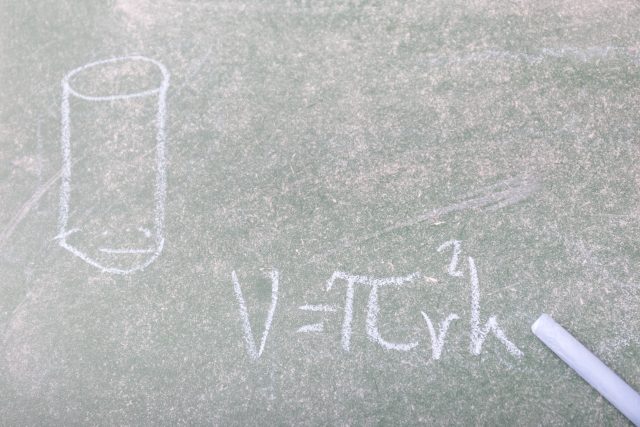 | |
 |  |  |
「円筒 形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
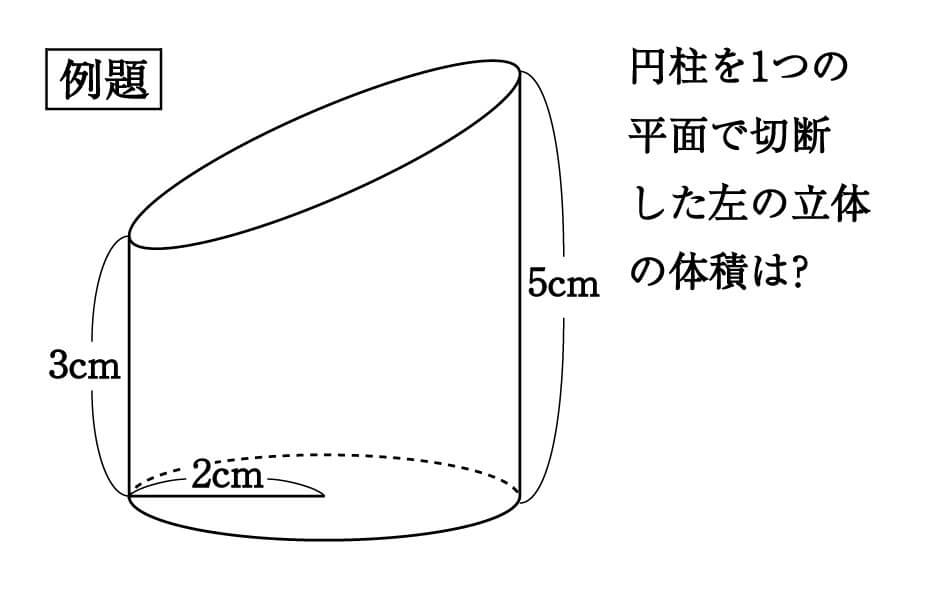 |  | |
「円筒 形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
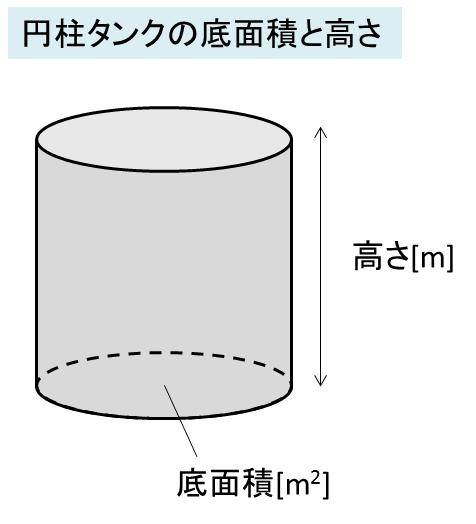
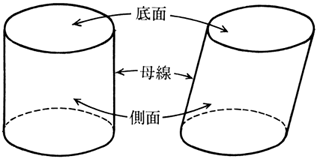 |  | |
 |  | |
「円筒 形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「円筒 形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「円筒 形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「円筒 形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「円筒 形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「円筒 形 体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
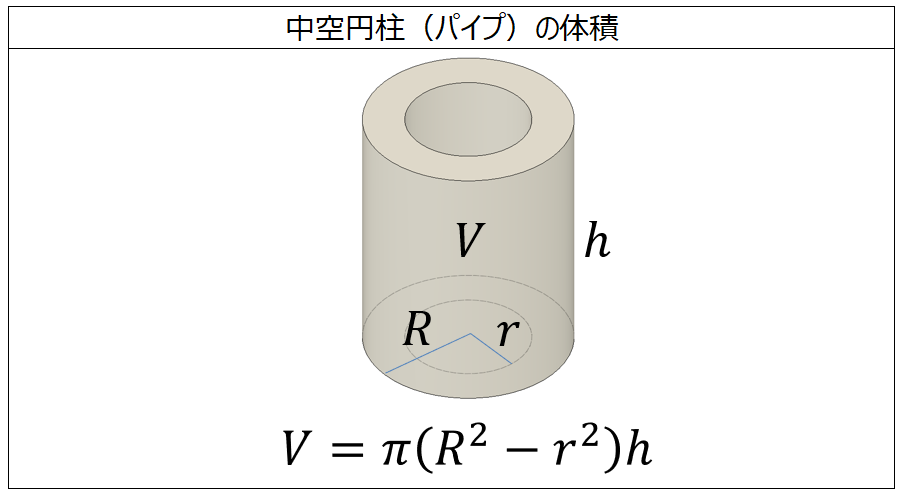
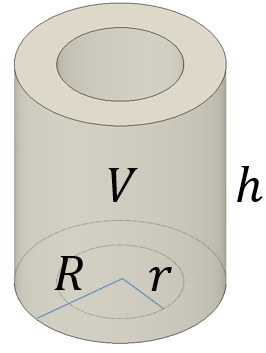
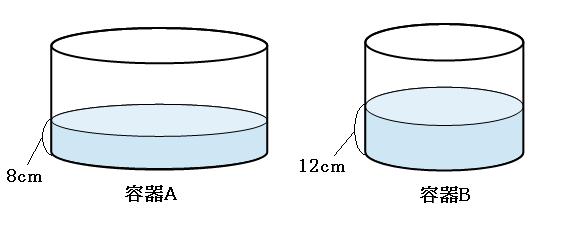
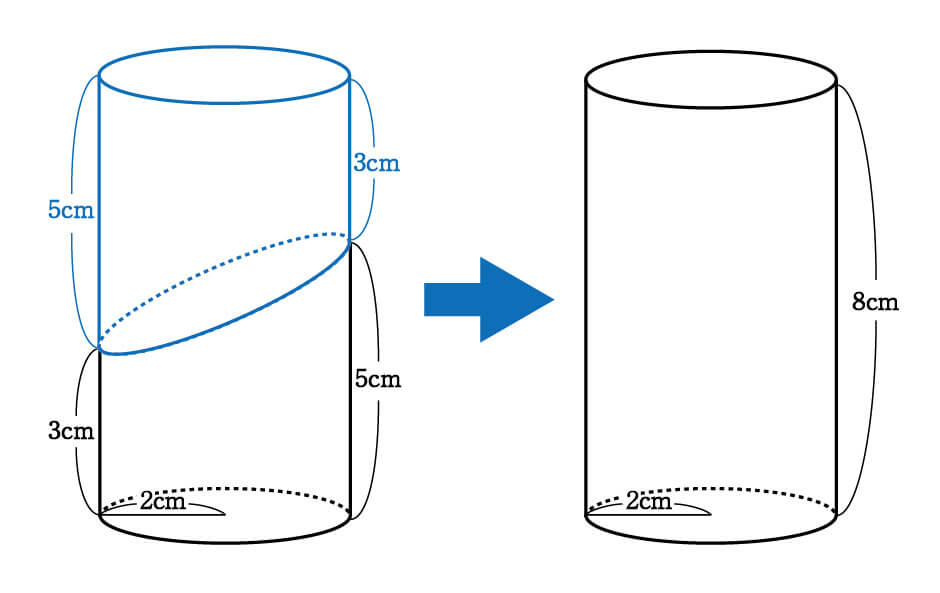
円筒形=円柱なら 半径×半径×314×高さですね。 要するに底面積×高さで柱の体積を求めます。 円筒形が 円柱の真ん中に空洞があるものを表しているなら。 下記の様に求めましょう 底面積 外円の面積-内円の面積で底面積が求めることができますね。 それに高さをかけた物が体積です。 2人 がナイス! しています taa******** taa******** さん小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題
コメント
コメントを投稿